This project uses Principal Component Analysis (PCA) to compress 100 unlabeled, sparse features into a more manageable number for classiying buyers of Ed Sheeran’s latest album.
Table of contents
- 00. Project Overview
- 01. Data Overview
- 02. PCA Overview
- 03. Data Preparation
- 04. Fitting PCA
- 05. Analysis Of Explained Variance
- 06. Applying our PCA solution
- 07. Classification Model
- 08. Growth & Next Steps
Project Overview
Context
The scenario is the grocery client looking to promote Ed Sheeran’s new album, targeting their customer communications, while being as efficient as possible with their marketing budget.
As a proof-of-concept, the client is interested in a classification model for customers who purchased Ed’s last album based upon a small sample of listening data they have acquired for some of their customers at that time.
If such a model is built successfully, the client will look to purchase up-to-date listening data, apply the model, and use the predicted probabilities to promote to customers who are most likely to purchase.
The sample data is short but wide. It contains only 356 customers, but for each, columns that represent the percentage of historical listening time allocated to each of 100 artists. On top of these, the 100 columns do not contain the artist in question, instead being labelled artist1, artist2 etc.
This data needs to be compressed into something more manageable for classification!
Actions
First, I brought in the required data, both the historical listening sample and the flag showing which customers purchased Ed Sheeran’s last album. I split the data into a training set & a test set, for classification purposes. For PCA, the data needs scaling so that all features exist on the same scale.
I then applied PCA without any specified number of components. This allowed me to examine & plot the percentage of explained variance for every number of components. Based upon this, I limited the dataset to the number of components that make up 75% of the variance of the initial feature set (rather than limiting to a specific number of components). I applied this rule to both the training set (using fit_transform) and the test set (using transform only).
With this new, compressed dataset, I applied a Random Forest Classifier to predict the sales of the album, and to assess the predictive performance.
Results
Based upon an analysis of variance vs. components, I decided to keep 75% of the variance of the initial feature set, which dropped the number of features from 100 down to 24.
Using these 24 components, I trained a Random Forest Classifier, which predicted customers that would purchase Ed Sheeran’s last album with a Classification Accuracy of 93%.
Growth/Next Steps
I only tested one type of classifier (Random Forest), but it would be worthwhile testing others. I also only used the default classifier hyperparameters and these would likely need further optimization.
With this instance, I selected 24 components based upon the fact this accounted for 75% of the variance of the initial feature set. Future instances would likely look to search for the optimal number of components to use based upon classification accuracy.
Data Overview
The dataset contains only 356 customers, but 102 columns.
In the code below, the steps are:
- Import the required python packages & libraries
- Import the data from the database
- Drop the ID column for each customer
- Shuffle the dataset
- Analyse the class balance between album buyers, and non album buyers
# import required Python packages
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# import data
data_for_model = ...
# drop the id column
data_for_model.drop("user_id", axis = 1, inplace = True)
# shuffle the data
data_for_model = shuffle(data_for_model, random_state = 42)
# analyse the class balance
data_for_model["purchased_album"].value_counts(normalize = True)
From the last step in the above code, the output reveals that 53% of customers in the sample purchased Ed’s last album, and 47% did not. Since this is evenly balanced, I relied solely on the metric Classification Accuracy when assessing the performance of the classification model later on.
Performing these steps yields a dataset that looks like the below sample (not all columns shown):
| purchased_album | artist1 | artist2 | artist3 | artist4 | artist5 | artist6 | artist7 | … |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0278 | 0 | 0 | 0 | 0 | 0.0036 | 0.0002 | … |
| 1 | 0 | 0 | 0.0367 | 0.0053 | 0 | 0 | 0.0367 | … |
| 1 | 0.0184 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 0 | 0.0017 | 0.0226 | 0 | 0 | 0 | 0 | 0 | … |
| 1 | 0.0002 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 1 | 0.0042 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 0 | 0 | 0 | 0.0002 | 0 | 0 | 0 | 0 | … |
| 1 | 0 | 0 | 0 | 0 | 0.1759 | 0 | 0 | … |
| 1 | 0.0001 | 0 | 0.0001 | 0 | 0 | 0 | 0 | … |
| 1 | 0 | 0 | 0 | 0.0555 | 0 | 0.0003 | 0 | … |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
The data is at customer level. There is a binary column showing whether the customer purchased the prior album or not, and then 100 columns containing the percentage of historical listening time allocated to each artist. The names of these artists are unknown.
From the above sample, the sparsity of the data is apparent; customers do not listen to all artists and therefore many of the values are 0.
PCA Overview
Principal Component Analysis (PCA) is often used as a Dimensionality Reduction technique that can reduce a large set of variables down to a smaller set, that still contains most of the original information.
In other words, PCA takes a high number of dimensions, or variables, and boils them down into a much smaller number of new variables, each of which is called a principal component. These new components are somewhat abstract in that they are a blend of some of the original features where the PCA algorithm found they were correlated. By blending the original variables rather than just removing them, the hope is that we still keep much of the key information that was held in the original feature set.
Dimensionality Reduction techniques like PCA are mainly used to simplify the space in which we’re operating. Attempting to apply the k-means clustering algorithm (for example) across hundreds or thousands of features can be computationally expensive. PCA reduces this while maintaining much of the key information contained in the data. But PCA doesn’t have applications just within the realms of unsupervised learning, it could just as easily be applied to a set of input variables in a supervised learning approach, exactly like in this project.
In supervised learning, we often focus on Feature Selection where we look to remove variables that are not deemed to be important in predicting our output. PCA is often used in a similar way, although in this case we aren’t explicitly removing variables - we are simply creating a smaller number of new ones that contain much of the information contained in the original set.
Business consideration of PCA: It is much more difficult to interpret the outputs of a predictive model (for example) that is based upon component values vs. the original variables.
Data Preparation
Split Out Data For Modeling
In the next code block, I do two things: Split the data into an X object which contains only the predictor variables, and a y object that contains only our dependent variable.
Then, split the data into training and test sets to ensure that I can fairly validate the accuracy of the predictions on data that was not used in training. In this case, I allocated 80% of the data for training, and the remaining 20% for validation. I added the stratify parameter to ensure that both the training and test sets have the same proportion of customers who did, and did not, sign up for the delivery club - this allows for more confidence in the assessment of predictive performance.
# split data into X and y objects for modelling
X = data_for_model.drop(["purchased_album"], axis = 1)
y = data_for_model["purchased_album"]
# split out training & test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42, stratify = y)
Feature Scaling
Feature Scaling is extremely important when applying PCA - it means that the algorithm can successfully “judge” the correlations between the variables and effectively create the principal compenents. The general consensus is to apply Standardization rather than Normalization as the scaling technique.
The below code uses the in-built StandardScaler functionality from scikit-learn to apply Standardization to all of our variables.
In the code, I use fit_transform for the training set, but only transform to the test set. This means the standardization logic will learn and apply the “rules” from the training data, but only apply them to the test data. This is important in order to avoid data leakage where the test set learns information about the training data, and means the model performance metrics can’t fully be trusted.
# create our scaler object
scale_standard = StandardScaler()
# standardise the data
X_train = scale_standard.fit_transform(X_train)
X_test = scale_standard.transform(X_test)
Fitting PCA
First, I applied PCA to the training set without limiting the algorithm to any particular number of components which means, at this point, that the feature space is not explicitly reduced.
Allowing all components to be created here allows for examining & plotting the percentage of explained variance for each, and assessing which solution might work best for the task, at hand.
In the code below, I instantiate the PCA object, and then fit it to the training set.
# instantiate our PCA object (no limit on components)
pca = PCA(n_components = None, random_state = 42)
# fit to our training data
pca.fit(X_train)
Analysis Of Explained Variance
There is no right or wrong number of components to use. This is something that needs decisions based upon the scenario we’re working in. We know we want to reduce the number of features, but we need to trade this off with the amount of information we lose.
In the following code, I extract this information from the prior step of fitting the PCA object to the training data. I extract the variance for each component, and I do the same again, but for the cumulative variance. I will assess & plot both of these in the next step.
# explained variance across components
explained_variance = pca.explained_variance_ratio_
# explained variance across components (cumulative)
explained_variance_cumulative = pca.explained_variance_ratio_.cumsum()
In the following code, I create two plots - one for the variance of each principal component, and one for the cumulative variance.
num_vars_list = list(range(1,101))
plt.figure(figsize=(16,9))
# plot the variance explained by each component
plt.subplot(2,1,1)
plt.bar(num_vars_list,explained_variance)
plt.title("Variance across Principal Components")
plt.xlabel("Number of Components")
plt.ylabel("% Variance")
plt.tight_layout()
# plot the cumulative variance
plt.subplot(2,1,2)
plt.plot(num_vars_list,explained_variance_cumulative)
plt.title("Cumulative Variance across Principal Components")
plt.xlabel("Number of Components")
plt.ylabel("Cumulative % Variance")
plt.tight_layout()
plt.show()
The top plot displays how PCA works in a way where the first component holds the most variance, and each subsequent component holds less and less.
The second plot shows this as a cumulative measure - and displays how many components would need to remain in order to keep any amount of variance from the original feature set.
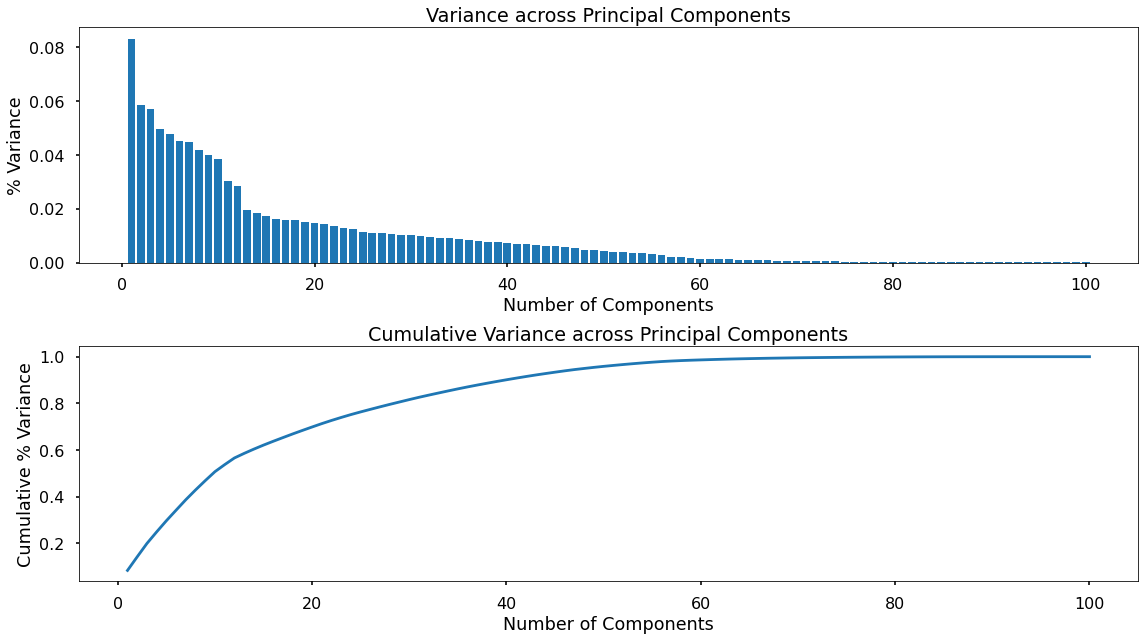
Based upon the cumulative plot above, 75% of the variance from the original feature set is kept with only around 25 components; in other words, with only a quarter of the number of features, we can still hold onto around three-quarters of the information.
Applying the PCA solution
In the code below, I re-instantiate the PCA object, this time specifying that I want the number of components that will keep 75% of the initial variance.
I then apply this solution to both the training set (using fit_transform) and the test set (using transform only).
Finally - based on this 75% threshold, I confirm the number of components that this leaves.
# re-instantiate our PCA object (keeping 75% of variance)
pca = PCA(n_components = 0.75, random_state = 42)
# fit to our data
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
# check the number of components
print(pca.n_components_)
Turns out, I was almost correct from looking at our chart - we will retain 75% of the information from our initial feature set, with only 24 principal components.
The X_train and X_test objects now contain 24 columns, each representing one of the principal components. A sample of X_train is below:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
|---|---|---|---|---|---|---|---|
| -0.402194 | -0.756999 | 0.219247 | -0.0995449 | 0.0527621 | 0.0968236 | -0.0500932 | … |
| -0.360072 | -1.13108 | 0.403249 | -0.573797 | -0.18079 | -0.305604 | -1.33653 | … |
| 10.6929 | -0.866574 | 0.711987 | 0.168807 | -0.333284 | 0.558677 | 0.861932 | … |
| -0.47788 | -0.688505 | 0.0876652 | -0.0656084 | -0.0842425 | 1.06402 | 0.309337 | … |
| -0.258285 | -0.738503 | 0.158456 | -0.0864722 | -0.0696632 | 1.79555 | 0.583046 | … |
| -0.440366 | -0.564226 | 0.0734247 | -0.0372701 | -0.0331369 | 0.204862 | 0.188869 | … |
| -0.56328 | -1.22408 | 1.05047 | -0.931397 | -0.353803 | -0.565929 | -2.4482 | … |
| -0.282545 | -0.379863 | 0.302378 | -0.0382711 | 0.133327 | 0.135512 | 0.131 | … |
| -0.460647 | -0.610939 | 0.085221 | -0.0560837 | 0.00254932 | 0.534791 | 0.251593 | … |
| … | … | … | … | … | … | … | … |
Here, column “0” represents the first component, column “1” represents the second component, and so on. These are the input variables to be fed into our classification model for predicting which customers purchased Ed Sheeran’s last album!
Classification Model
Training The Classifier
To start with, I apply a Random Forest Classifier to see if it is possible to predict based upon the set of 24 components.
In the code below, I instantiate the Random Forest using the default parameters, and then fit this to the data.
# instantiate our model object
clf = RandomForestClassifier(random_state = 42)
# fit our model using our training & test sets
clf.fit(X_train, y_train)
Classification Performance
In the code below, I use the trained classifier to predict on the test set and run a simple analysis for the classification accuracy for the predictions vs. actuals.
# predict on the test set
y_pred_class = clf.predict(X_test)
# assess the classification accuracy
accuracy_score(y_test, y_pred_class)
The result of this is a 93% classification accuracy. This means, by using a classifier trained on 24 principal components, the model accurately predicted which test set customers purchased Ed Sheeran’s last album, with an accuracy of 93%.
Application
Based upon this proof-of-concept, the recommendation could be made to the client that they purchase some up to date listening data. PCA could be applied to this, the components could be created, and predictions for which customers are likely to buy Ed’s next album could occur.
Growth & Next Steps
I only tested one type of classifier here (Random Forest) and it would be worthwhile to testothers. I also only used the default classifier hyperparameters and these would likely be further optimized.
Here, I selected 24 components based upon the fact that these accounted for 75% of the variance of the initial feature set. Future work would involve searching for the optimal number of components to use based upon classification accuracy.